Comment utiliser un nuage de points dans Microsoft Excel pour prédire le comportement des données ?

Une analyse efficace des données nécessite une compréhension claire de la relation entre les variables et les quantités impliquées. Et si vous disposez de bonnes données, vous pouvez même les utiliser pour prédire leur comportement.

Cependant, à moins d’être un mathématicien, il est extrêmement difficile de créer une équation à partir d’un ensemble de données. Mais avec Microsoft Excel, presque tout le monde peut le faire en utilisant un nuage de points. Voici comment.

Création d’un graphique en nuage de points dans Microsoft Excel

Avant de pouvoir prédire une tendance, vous devez d’abord créer un diagramme de dispersion pour en trouver une. Le graphique en nuage de points présente la relation entre deux variables le long des deux axes du graphique, avec une variable indépendante et l’autre dépendante.

La variable indépendante est généralement affichée sur l’axe horizontal du graphique, tandis que vous pouvez trouver la variable dépendante sur son axe vertical. La relation entre les deux est alors représentée par la ligne du graphique.

Pour créer un graphique en nuage de points sur une feuille Excel, suivez les étapes ci-dessous :

1. Ouvrez la feuille de calcul contenant les données que vous souhaitez tracer sur le graphique en nuage de points.
2. Placez la variable indépendante dans la colonne de gauche et la variable dépendante dans la colonne de droite.
3. Sélectionnez la valeur des deux colonnes que vous voulez tracer.
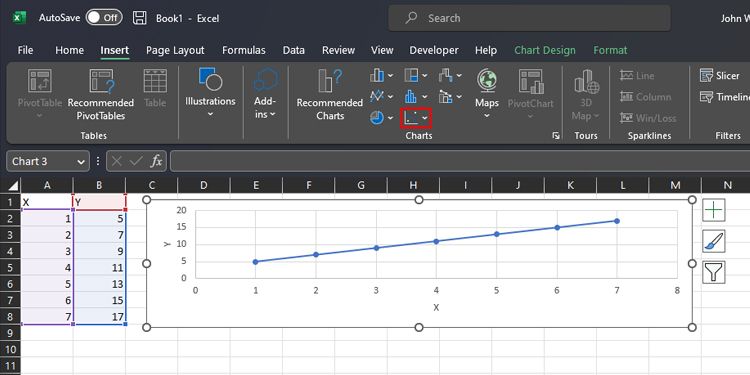
4. Cliquez sur le bouton Insérer Onglet et aller à Graphiques groupe. Cliquez maintenant sur Insérer un diagramme de dispersion (X, Y) ou un diagramme à bulles..
5. Ici, vous trouverez différents styles de diagramme de dispersion. Choisissez l’un d’entre eux en cliquant dessus.
6. Le graphique s’affiche à l’écran. Changez le nom des axes et le titre du graphique.

   

Dessiner une ligne de tendance sur un graphique en nuage de points

Afin de présenter la relation entre les variables du graphique, une ligne de tendance est nécessaire. La ligne de tendance doit être similaire ou se superposer aux valeurs des données du graphique afin d’estimer avec précision la relation entre les variables. Pour dessiner une ligne de tendance sur le graphique de dispersion :

1. Cliquez avec le bouton droit de la souris sur n’importe quel point de données du graphique en nuage de points.
2. Dans la liste d’options qui apparaît, sélectionnez Ajouter une ligne de tendance.
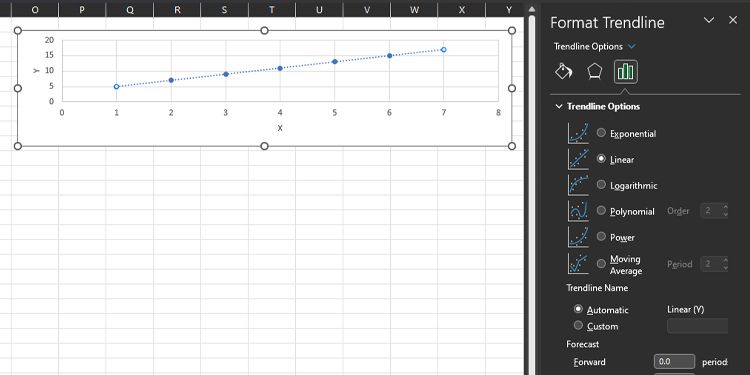
3. A Format Trendline s’ouvrira sur le côté droit avec la fenêtre Linéaire option sélectionnée par défaut.

   

Cette opération permet d’ajouter une ligne de tendance (ligne droite en pointillés) à votre graphique en nuage de points.

Options de formatage de la ligne de tendance pour ajuster la courbe des valeurs de données

Nous voulons ajuster la courbe de tendance aussi près que possible du tracé de la courbe. De cette façon, nous pouvons avoir un aperçu de la relation approximative entre les variables. Pour ce faire, suivez les étapes ci-dessous :

1. Choisissez différentes courbes parmi OPTIONS DE LIGNES DE TENDANCE dans le Format Trendline pour ajuster la courbe de tendance avec un tracé de courbe.
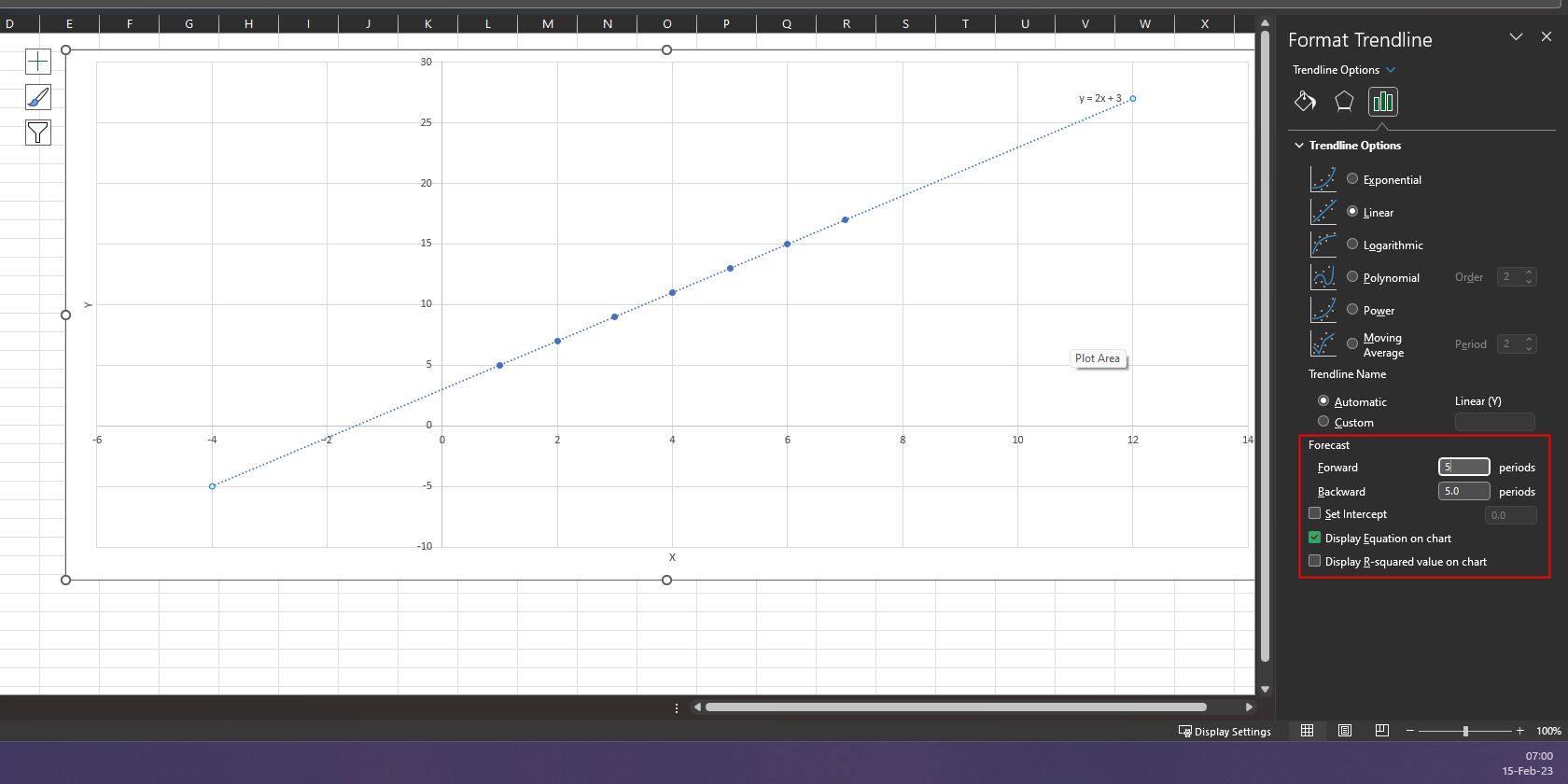
2. Cochez la case Afficher l’équation sur le graphique Cochez cette case pour afficher l’équation de l’ajustement de la courbe sur le graphique en nuage de points.

Prévision des valeurs avant et arrière sur la base des tendances

Après l’ajustement de la courbe, vous pouvez utiliser cette ligne de tendance pour prévoir les valeurs précédentes et futures qui ne font pas partie de cet ensemble de données. Pour ce faire, attribuez une valeur dans la section Forecast de la fenêtre Format Trendline. Ajoutez les périodes souhaitées dans la section Forward et Retour en arrière pour observer les valeurs attendues sur le graphique en nuage de points.

Prévision de la relation entre plusieurs variables indépendantes et dépendantes pour formuler une équation

Les données contiennent parfois plusieurs variables indépendantes qui créent des valeurs résultantes. Dans de tels cas, la tendance peut ne pas être directe. Pour identifier la relation, vous devrez peut-être rechercher des tendances parmi la quantité dépendante et les variables indépendantes individuelles.

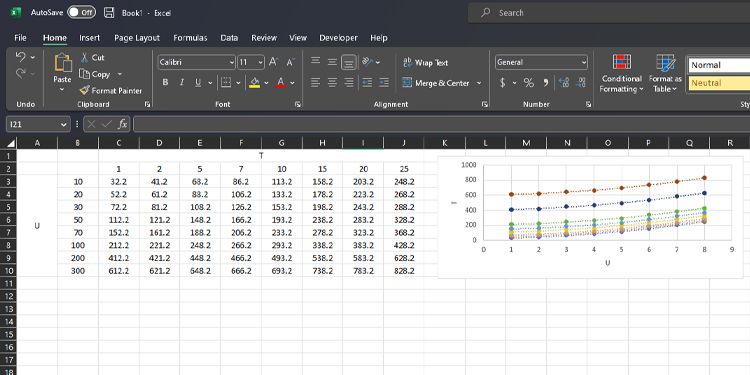
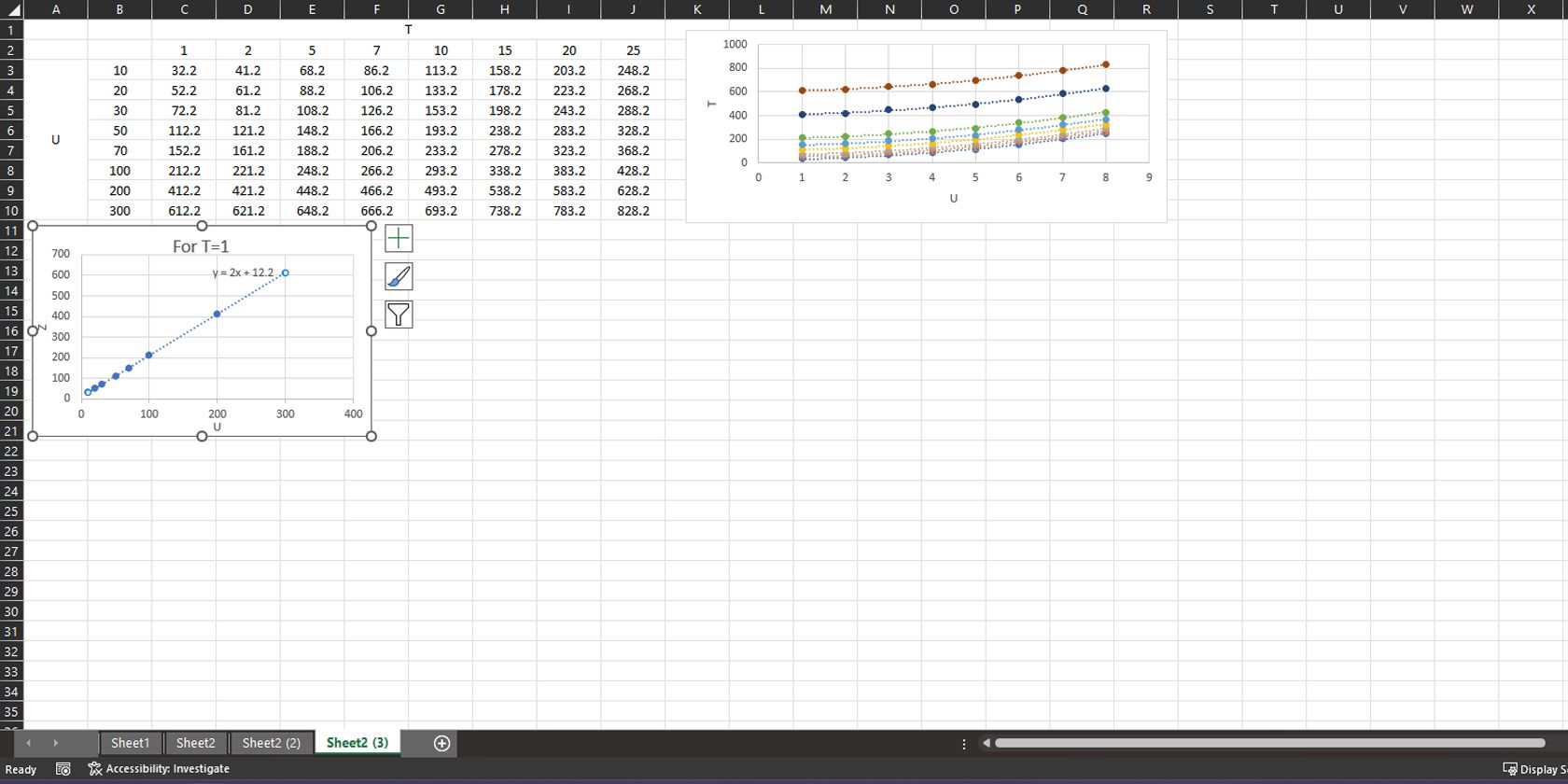
Dans la figure ci-dessous, nous avons un ensemble de données qui contient deux variables indépendantes. Dans le graphique, l’axe horizontal représente la variable u et l’axe vertical représente la variable dépendante résultante. Chaque ligne du graphique est également une fonction de la variable T.

Ici, nous allons trouver un moyen de trouver la relation approximative entre la variable dépendante Y(U,T) (ou valeur résultante) et les variables indépendantes U et T. Cela nous permettrait d’extrapoler les valeurs de ces variables pour prédire le comportement des données.

Pour ce faire, suivez les étapes ci-dessous :

1. Premièrement, nous allons trouver la relation entre une variable indépendante (U) et la résultante dépendante Y. Conservez la valeur des autres valeurs indépendantes (T) constante en ne choisissant qu’une seule colonne à la fois.
2. Sélectionner les cellules B3 à B10 pour sélectionner U et Cellules C3 à C10 (valeur résultante à T=1) et utilisez un diagramme de dispersion pour les représenter.
3. Tracez maintenant la ligne de tendance et utilisez la ligne de tendance la mieux ajustée montrée dans le graphique de dispersion. Format de la ligne de tendance qui s’adapte à l’ensemble des données. Dans ce cas, nous avons observé que la ligne de tendance « linéaire » correspond le mieux à la courbe.
4. Cliquez sur Afficher l’équation sur le graphique dans le Format Trendline fenêtre de la ligne.
5. Renommez les axes du graphique en fonction des variables de données.

   

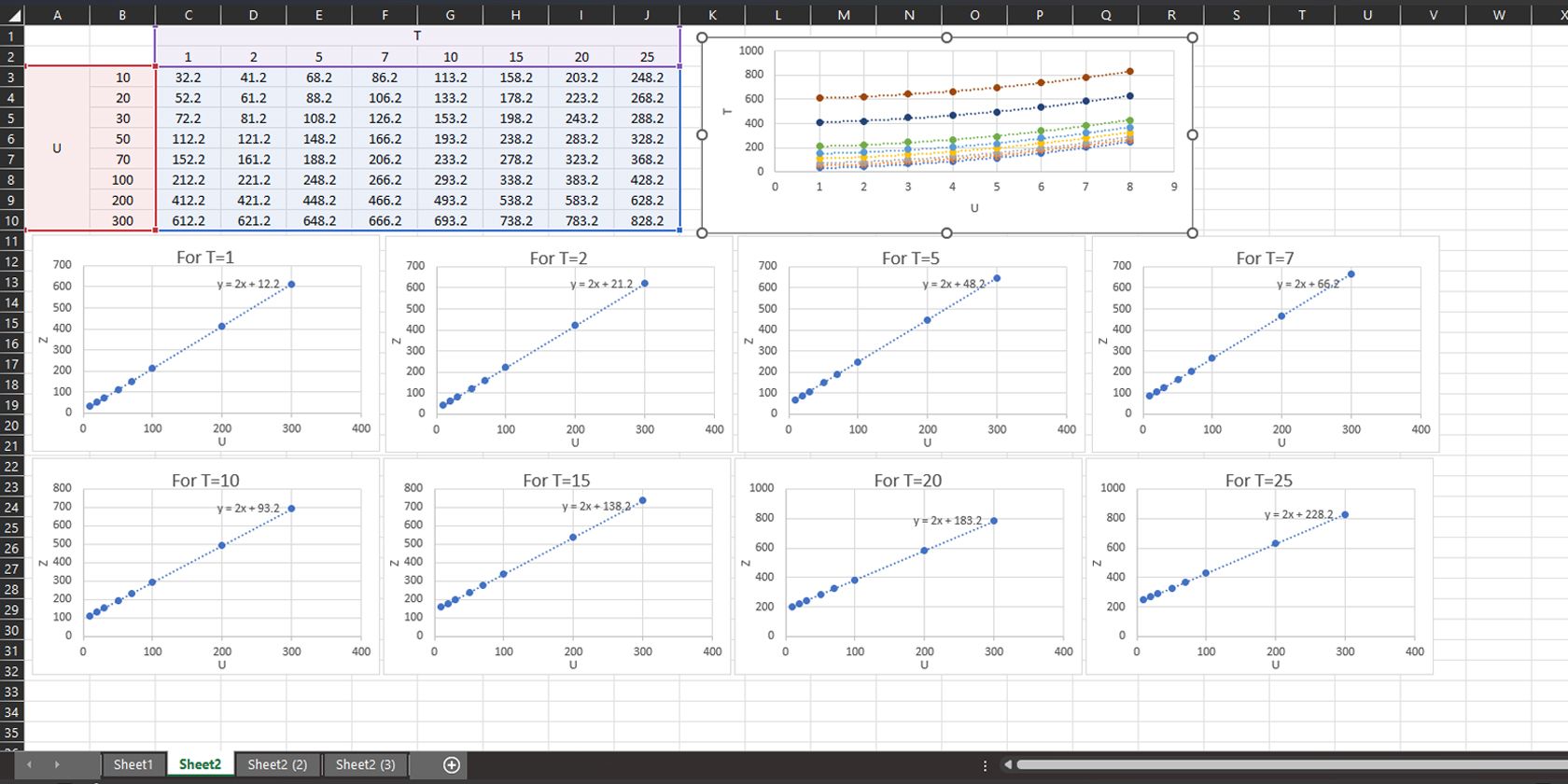
6. Ensuite, vous devez créer un diagramme de dispersion pour toutes les autres variables sous T. Suivez les étapes 1 à 5, mais choisissez des colonnes D3 à D10 (T=2), E3 à E10 (T=5), F3 à F10 (T=7), G3 à G10 (T=10), H3 à H10 (T=15), I3 à I10 (T=20) et J3 à J10 (T=20) séparément avec la variable U contenant des cellules B3 à B10.

   

7. Vous devriez trouver les équations suivantes affichées sur les graphiques.

   T	Y
   T=1	Y=2U+12.2
   T=2	Y=2U+21.2
   T=5	Y=2U+48.2
   T=7	Y=2U+66.2
   T=10	Y=2U+93.2
   T=15	Y=2U+138.2
   T=20	Y=2U+183.2
   T=25	Y=2U+228.2

   Nous pouvons observer que toutes les équations sont linéaires et ont le même coefficient sur la variable U. Cela nous rapproche de la conclusion que Y est égal à 2U et d’autres valeurs différentes qui peuvent être fonction de la variable T.

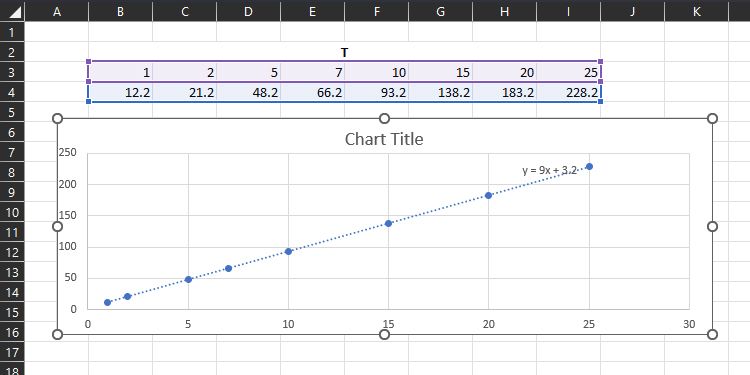
8. Notez ces valeurs séparément et disposez-les comme indiqué ci-dessous (chaque valeur avec sa valeur variable notée, par exemple 12.2 avec T=1 et 228 avec T=25etc.). Maintenant, tracez un nuage de points de ces valeurs et affichez l’équation représentant la relation entre ces valeurs et la variable T.

   

9. Enfin, nous pouvons relier Y(U,T) comme

 Y(U,T)=2U+9T+3.2 

Vous pouvez vérifier ces valeurs en traçant cette équation pour différentes valeurs de U et T. De même, vous pouvez prédire le comportement de Y(U,T) pour différentes valeurs des variables U et T non disponible avec cet ensemble de données.

Vous n’avez pas besoin d’être un expert en mathématiques pour prédire les tendances avec Microsoft Excel.

Maintenant que vous savez comment trouver la relation entre une fonction et ses conditions dépendantes, vous pouvez tirer des conclusions valables sur le comportement de la fonction. Si vous disposez de toutes les variables nécessaires qui affectent la fonction mathématique, vous pouvez prédire avec précision sa valeur dans les conditions données.

Microsoft Excel est un excellent outil qui vous permet également de tracer des fonctions multivariables. Maintenant que vous avez vos données, vous devriez également explorer les différentes façons de créer des graphiques et des diagrammes puissants pour les présenter.